Dersimix Eğitim Harmanı

KOMBİNASYON NEDİR?

Kombinasyon, bir nesne grubu içerisinden, sıra gözetmeksizin yapılan seçimlerdir.Diğer bir deyişle nesne grubuna karşılık gelen kümenin alt kümeleri olarak da adlandırılır. Çünkü, alt kümelerde sıra önemli değildir. O halde şöyle tanımlanabilir: Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Örneğin, 24 öğrenci arasından seçeceğiniz 5 öğrenci, öğrencileri seçme sıranız önemli olmadığından bir kombinasyon problemidir.

Tanım : r ve n pozitif doğal sayılar ve r £ n olmak şartıyla n elemanlı bir A kümesinin r elemanlı alt kümelerinin her birine, A kümesinin r ’ li kombinasyonudenir.

n elemanlı kümenin r’li kombinasyonlarının sayısı, C(n,r) ya da (ⁿ_r ) ile gösterilir.

n elemanlı kümenin r ' li kombinasyonları sayısının formülü,

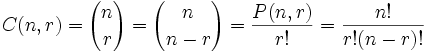
$C(n,r)={n choose r} = {n choose {n-r}} = frac{P(n,r)}{r!} = frac{n!}{r!(n - r)!}$

Örnek:
$C(5,3)={5 choose 3}={5 choose {5-3}} = frac{P(5,3)}{3!} = frac{5!}{3!(5 - 3)!}=10$

UYARI :Permütasyonda sıralama, kombinasyonda ise seçme sözkonusudur.

Çözümlü Örnek Sorular